There are two popular styles of Sigma control charts. One plots the subgroup’s standard deviation and the other plots the estimate of the population’s standard deviation, inferred from the subgroup’s standard deviation. The subgroup’s standard deviation is referred to as "sigma" or σ and the population’s standard deviation inferred from the subgroup is referred to as "s". Both calculations use "n", the subgroup size. Both calculations also use each element of the subgroup, referred to as X1, X2, … Xn, and the subgroup average, referred to as XBar.
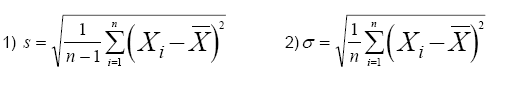
Many people wonder which equation they should use. The answer is, you can use either, as long as you are consistent.

In fact, both graphs look identical except for a scale factor. Control limits also differ by the same scale factor, so any subgroup reported as in control by one method will also be in control by the other, and any subgroup reported as out of control by one method will also be out of control by the other. Less obvious is the effect your choice of styles has on the calculation of XBar limits. XBar control limits are calculated from an estimate of the process mean and standard deviation. Both formulas are given below:
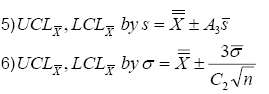
Substituting equation 4) into equation 5) gives us equation 7).
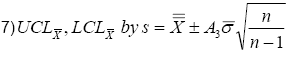
We see 5) and 6) are equal if and only if 6) and 7) are equal, and 6) and 7) are equal if, and only if, 8) is true. We test 8) with 9).

So we calculate Test for values of n from 2 to 25 and compare them to A3. A3, C2, and Test for n=2 to 25 are listed below.
As you can see, both the sample and the population calculations work, and give the same result. For details of the “sigma” style, refer to ASQC standard A1-1971, for details of the “s” style, refer to Juran’s Quality Control Handbook.